September 3rd, 2016 | 2 Comments
Matplotlib has four new colormaps called viridis, plasma, magma, and inferno. Especially viridis you might have seen already as this will be the new default in Matplotlib 2.0. They are freely available and now also included in the gnuplot-palettes repository on github. They are well designed to be perceptually uniform and friendly for common forms of colorblindness, so they should be save to use as your default colormap. Personally I would not recommend them for every kind of plot as they are a little dark if you have large areas with low values in your plot.
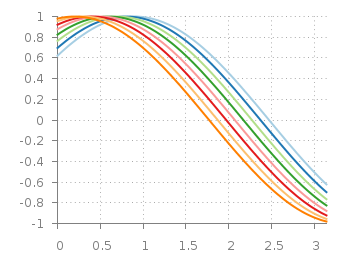
As usual in the gnuplot-palettes repository they are accompanied by line style definitions using the palette colors.
# viridis set style line 1 lt 1 lc rgb '#440154' # dark purple set style line 2 lt 1 lc rgb '#472c7a' # purple set style line 3 lt 1 lc rgb '#3b518b' # blue set style line 4 lt 1 lc rgb '#2c718e' # blue set style line 5 lt 1 lc rgb '#21908d' # blue-green set style line 6 lt 1 lc rgb '#27ad81' # green set style line 7 lt 1 lc rgb '#5cc863' # green set style line 8 lt 1 lc rgb '#aadc32' # lime green set style line 9 lt 1 lc rgb '#fde725' # yellow
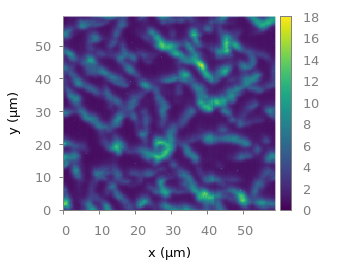
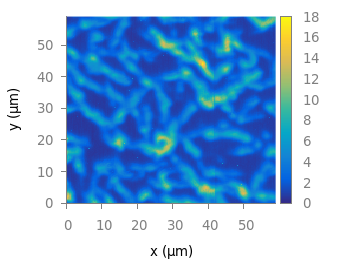
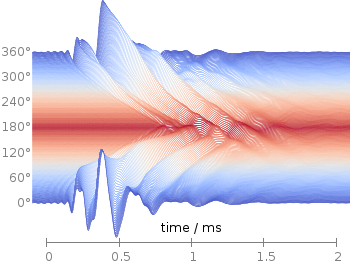
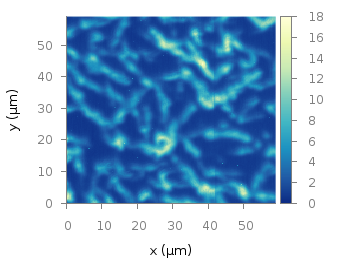
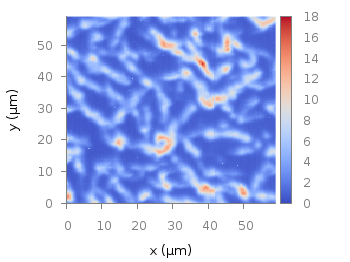
Fig. 1 Photoluminescence yield plotted with the viridis colormap from Matplotlib (code to produce this figure, viridis.pal, data)
# plasma set style line 1 lt 1 lc rgb '#0c0887' # blue set style line 2 lt 1 lc rgb '#4b03a1' # purple-blue set style line 3 lt 1 lc rgb '#7d03a8' # purple set style line 4 lt 1 lc rgb '#a82296' # purple set style line 5 lt 1 lc rgb '#cb4679' # magenta set style line 6 lt 1 lc rgb '#e56b5d' # red set style line 7 lt 1 lc rgb '#f89441' # orange set style line 8 lt 1 lc rgb '#fdc328' # orange set style line 9 lt 1 lc rgb '#f0f921' # yellow
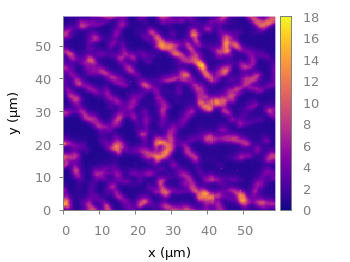
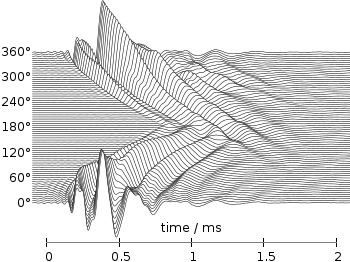
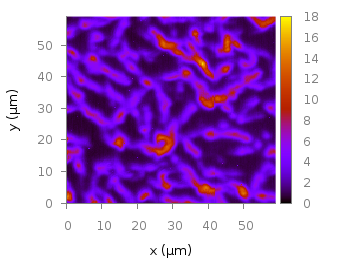
Fig. 2 Photoluminescence yield plotted with the plasma colormap from Matplotlib (code to produce this figure, plasma.pal, data)
# magma set style line 1 lt 1 lc rgb '#000004' # black set style line 2 lt 1 lc rgb '#1c1044' # dark blue set style line 3 lt 1 lc rgb '#4f127b' # dark purple set style line 4 lt 1 lc rgb '#812581' # purple set style line 5 lt 1 lc rgb '#b5367a' # magenta set style line 6 lt 1 lc rgb '#e55964' # light red set style line 7 lt 1 lc rgb '#fb8761' # orange set style line 8 lt 1 lc rgb '#fec287' # light orange set style line 9 lt 1 lc rgb '#fbfdbf' # light yellow
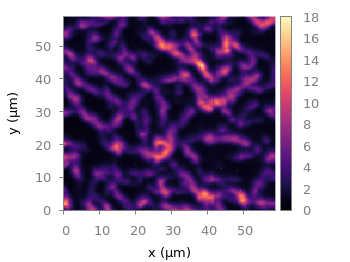
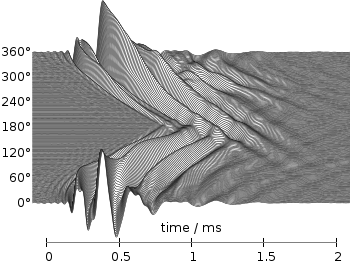
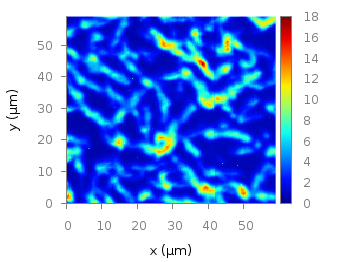
Fig. 3 Photoluminescence yield plotted with the magma colormap from Matplotlib (code to produce this figure, magma.pal, data)
# inferno set style line 1 lt 1 lc rgb '#000004' # black set style line 2 lt 1 lc rgb '#1f0c48' # dark purple set style line 3 lt 1 lc rgb '#550f6d' # dark purple set style line 4 lt 1 lc rgb '#88226a' # purple set style line 5 lt 1 lc rgb '#a83655' # red-magenta set style line 6 lt 1 lc rgb '#e35933' # red set style line 7 lt 1 lc rgb '#f9950a' # orange set style line 8 lt 1 lc rgb '#f8c932' # yellow-orange set style line 9 lt 1 lc rgb '#fcffa4' # light yellow
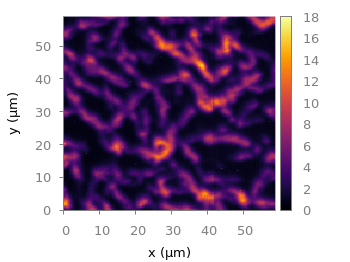
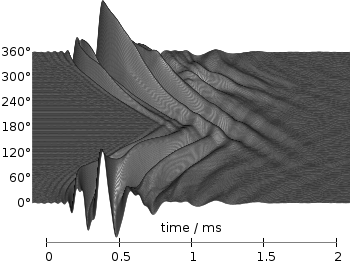
Fig. 4 Photoluminescence yield plotted with the inferno colormap from Matplotlib (code to produce this figure, inferno.pal, data)