Gnuplotting

September 23rd, 2016 | 4 Comments

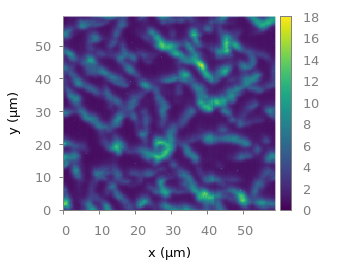
Suppose you have a large circular container filled with sand and measure its density at different positions. Now the goal is to display your measurements as a heat map extrapolated from your measurements, but limiting that heat map to the inner part of the container as shown in Fig. 1.

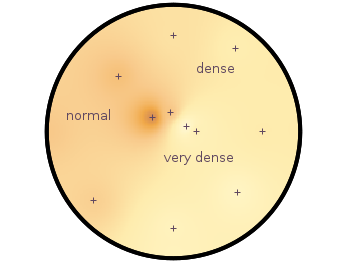
Fig. 1 Sand density measured at different positions in a circular container (code to produce this figure, sand.pal, data)

The underlying measurements are provided in the following format:

# sand_density_orig.txt
#1      2        3        4      5       6
#prob   x        y        z      density description
"E01"   0.00000 -1.14161 -0.020  0.7500  "dense"
"E02"  -0.94493 -0.81804 -0.020  0.5753  "normal"
"E03"   0.75306 -0.72000 -0.020  0.7792  "dense"
...

Those data points have to be extrapolated onto a grid for the heat map, which can be achieved by the following commands.

set view map
set pm3d at b map
set dgrid3d 200,200,2
splot "sand_density1.txt" u 2:3:5

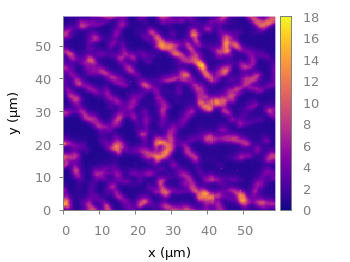
Fig. 2 shows the result which has two problems. The grid data is limited to the boundary given by the measurement points. In addition, the grid is always rectangular in size and not circular.

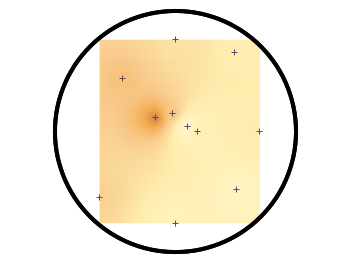
Fig. 2 Sand density measured at different positions in a circular container (code to produce this figure, sand.pal, data)

To overcome the first problem you have to add four additional points to the original data in order to stretch the grid boundary to the radius of the container. For that you have to come up with some reasonable extrapolation from the existing points. I did this in a very simple way by a mixture of linear interpolation or using the value of the nearest point. If you want to do the same with your data set you should maybe spent a little bit more effort on this.

# sand_density.txt
#1      2        3        4      5       6
#prob   x        y        z      density description
"E01"   0.00000 -1.14161 -0.020  0.7500  "dense"
...
"xmin" -1.50000  0.00000 -0.050  0.5508  "dummy"
"xmax"  1.50000  0.00000 -0.050  0.6634  "dummy"
"ymin"  0.00000 -1.50000 -0.050  0.7500  "dummy"
"ymax"  0.00000  1.50000 -0.050  0.6315  "dummy"

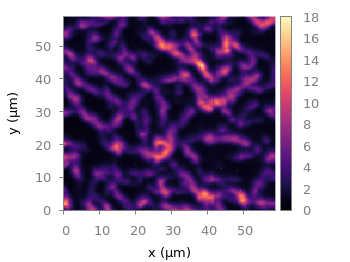
If you plot those modified data set you will get Fig. 3.

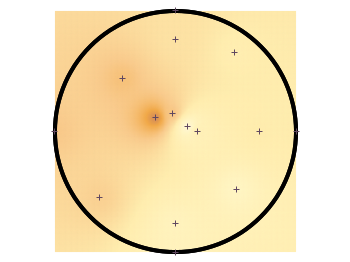
Fig. 3 Sand density measured at different positions in a circular container (code to produce this figure, sand.pal, data)

In order to limit the heat map to a circle you first extrapolate the grid using dgrid3d and store the data in a new file.

set table "tmp.txt"
set dgrid3d 200,200,2
splot "sand_density2.txt" u 2:3:5
unset table

Afterwards a function is defined in order to limit the points to the inner of the circle and plot the data from the temporary file.

circle(x,y,z) = sqrt(x**2+y**2)>r ? NaN : z
plot "tmp.txt" u 1:2:(circle($1,$2,$3)) w image

Finally a few labels and the original measurement points are added. The manually added points like xmin are removed by a smaller radius value. The result is then the nice circular heat map in Fig. 1.

r = 1.49 # make radius smaller to exclude interpolated edge points
set label 'normal' at -1,0.2 center front tc ls 1
set label 'dense' at 0.5,0.75 center front tc ls 1
set label 'very dense' at 0.3,-0.3 center front tc ls 1
plot "sand_density.txt" \
         u (circle($2,$3,$2)):(circle($2,$3,$3)) w p ls 1

Tags: circle, colormap, dgrid3d, grid, image

September 3rd, 2016 | 2 Comments

Matplotlib has four new colormaps called viridis, plasma, magma, and inferno. Especially viridis you might have seen already as this will be the new default in Matplotlib 2.0. They are freely available and now also included in the gnuplot-palettes repository on github. They are well designed to be perceptually uniform and friendly for common forms of colorblindness, so they should be save to use as your default colormap. Personally I would not recommend them for every kind of plot as they are a little dark if you have large areas with low values in your plot.

As usual in the gnuplot-palettes repository they are accompanied by line style definitions using the palette colors.

# viridis
set style line  1 lt 1 lc rgb '#440154' # dark purple
set style line  2 lt 1 lc rgb '#472c7a' # purple
set style line  3 lt 1 lc rgb '#3b518b' # blue
set style line  4 lt 1 lc rgb '#2c718e' # blue
set style line  5 lt 1 lc rgb '#21908d' # blue-green
set style line  6 lt 1 lc rgb '#27ad81' # green
set style line  7 lt 1 lc rgb '#5cc863' # green
set style line  8 lt 1 lc rgb '#aadc32' # lime green
set style line  9 lt 1 lc rgb '#fde725' # yellow

Fig. 1 Photoluminescence yield plotted with the viridis colormap from Matplotlib (code to produce this figure, viridis.pal, data)

# plasma
set style line  1 lt 1 lc rgb '#0c0887' # blue
set style line  2 lt 1 lc rgb '#4b03a1' # purple-blue
set style line  3 lt 1 lc rgb '#7d03a8' # purple
set style line  4 lt 1 lc rgb '#a82296' # purple
set style line  5 lt 1 lc rgb '#cb4679' # magenta
set style line  6 lt 1 lc rgb '#e56b5d' # red
set style line  7 lt 1 lc rgb '#f89441' # orange
set style line  8 lt 1 lc rgb '#fdc328' # orange
set style line  9 lt 1 lc rgb '#f0f921' # yellow

Fig. 2 Photoluminescence yield plotted with the plasma colormap from Matplotlib (code to produce this figure, plasma.pal, data)

# magma
set style line  1 lt 1 lc rgb '#000004' # black
set style line  2 lt 1 lc rgb '#1c1044' # dark blue
set style line  3 lt 1 lc rgb '#4f127b' # dark purple
set style line  4 lt 1 lc rgb '#812581' # purple
set style line  5 lt 1 lc rgb '#b5367a' # magenta
set style line  6 lt 1 lc rgb '#e55964' # light red
set style line  7 lt 1 lc rgb '#fb8761' # orange
set style line  8 lt 1 lc rgb '#fec287' # light orange
set style line  9 lt 1 lc rgb '#fbfdbf' # light yellow

Fig. 3 Photoluminescence yield plotted with the magma colormap from Matplotlib (code to produce this figure, magma.pal, data)

# inferno
set style line  1 lt 1 lc rgb '#000004' # black
set style line  2 lt 1 lc rgb '#1f0c48' # dark purple
set style line  3 lt 1 lc rgb '#550f6d' # dark purple
set style line  4 lt 1 lc rgb '#88226a' # purple
set style line  5 lt 1 lc rgb '#a83655' # red-magenta
set style line  6 lt 1 lc rgb '#e35933' # red
set style line  7 lt 1 lc rgb '#f9950a' # orange
set style line  8 lt 1 lc rgb '#f8c932' # yellow-orange
set style line  9 lt 1 lc rgb '#fcffa4' # light yellow

Fig. 4 Photoluminescence yield plotted with the inferno colormap from Matplotlib (code to produce this figure, inferno.pal, data)

Tags: colormap, linestyle, load, palette

April 13th, 2015 | 3 Comments

Instead of using a legend it is often a good idea to label your data directly in the graph. If you use a grid it can happen that you want to use a white background with your labels. This would improve the readability of the labels as it reduces interaction with the grid. To add a background is not straightforward, especially if you have rotated labels. In the following, we will have a look how to solve the problem for LaTeX terminals. Thanks to V. Mózer for the idea and the data for the plot. Fig. 1 presents the desired result.

Fig. 1 Fire severity as given by the fire temperature over time for a real vs. normalized fire. Click on the figure to see the original PDF version. (code to produce this figure, data)

To add a background to the labels we use the colorbox command, which we include in our terminal definition via the header option.

set terminal cairolatex standalone pdf size 16cm,10.5cm dashed transparent \
monochrome header monochrome \
header '\newcommand{\hl}[1]{\setlength{\fboxsep}{0.75pt}\colorbox{white}{#1}}'

In addition, we specify the size of the background area with the \setlength{\fboxsep}{0.75pt} command. This is quite handy as the default background size of \colorbox is a little to large for labels.

For the labels themselves, we only have to highlight them with the \hl{} command to get the desired background.

set label 1 at  50, 250 '\hl{\small $t_\textrm{Nc}$}' center rotate by 45 front

Fig. 2 Fire severity as given by the fire temperature over time for a real vs. normalized fire. Click on the figure to see the original PDF version.(code to produce this figure, data)

If you have a label with a line break, you have to decide if you want to apply the background to every part of the line break, as shown in Fig. 1

set label 2 at  90, 100 '\small \shortstack[l]{\hl{Temperature of reference '.\
                        'point} \\ \hl{during construction $t_\textrm{Nc} / '.\
                        't_\textrm{rc}$}}' front

or if you want to highlight the whole label without seeing some grid between the lines

set label 2 at  90, 100 '\hl{\small \shortstack[l]{Temperature of '.\
                        'reference point \\ during construction '.\
                        '$t_\textrm{Nc} / t_\textrm{rc}$}}' front

Fig. 2 shows the result for that one.

Tags: background, cairolatex, epslatex, label

March 2nd, 2015 | 4 Comments

If you are a regular gnuplot user you most probably want to reuse some common settings. I normally avoid it on this blog to have easy scripts that run as standalone files, but during my work I use a lot of small config files.

Fig. 1 Bessel functions from order zero up to six plotted with the dark2 line colors. (code to produce this figure, dark2.pal, xyborder.cfg, grid.cfg, mathematics.cfg)

Let us start with the Bessel function example from the last blog entry. As you can see in Fig. 1, it is a 2D plot, including axes, a grid, line colors, and definitions of higher order Bessel functions. All of those could be easily stored in small config files and reused in other plots.
As an example I will start with the axes. Here, I have four different config files, called xyborder.cfg, xborder, yborder.cfg, noborder.cfg, which do exactly what their names would suggest. Here are the first and last file:

# xyborder.cfg
set style line 101 lc rgb '#808080' lt 1 lw 1
set border 3 front ls 101
set tics nomirror out scale 0.75
set format '%g'

# noborder.cfg
set border 0
set style line 101 lc rgb '#808080' lt 1 lw 1
unset xlabel
unset ylabel
set format x ''
set format y ''
set tics scale 0

In the main plotting file I then just have to load the setting I like to have and I’m done. The same can be done for adding a grid, the right line color definitions and the extra Bessel functions leading to the following excerpt from the main plotting file:

# set path of config snippets
set loadpath './config'
# load config snippets
load 'dark2.pal'
load 'xyborder.cfg'
load 'grid.cfg'
load 'mathematics.cfg'

The set loadpath command tells gnuplot the directory where it can find all the configuration snippets. If you want to see an overview, look at my gnuplot configuration snippets and at the collection of palettes and line colors.

Fig. 2 (code to produce this figure, moreland.pal, noborder.cfg, arrows.cfg)

If you want to include more complicated settings, you have to use the macro setting of gnuplot. Fig. 2 is a reproduction of an earlier entry plotting a vector field with arrows. It included an lenghty definition of how to plot these arrows. If you want to do it several time and define the arrows in the same way every time you should also put it into a config file, this time as a variable (macro). In our example it looks like

color_arrows = 'u ($1-dx($1,$2)/2.0):($2-dy($1,$2)/2.0):(dx($1,$2)):(dy($1,$2)):\
(v($1,$2)) with vectors head size 0.08,20,60 filled lc palette'

In the main file the only thing we have then to do is

set macros
load 'noborder.cfg'
load 'moreland.pal'
load 'arrows.cfg'

# [...] 

plot '++' @color_arrows

Important is the first line that enables the use of macros in gnuplot which is disabled by default.

Tags: arrow, border, configuration, grid, palette, vectors

January 8th, 2015 | 9 Comments

Some time ago I discussed how to get the jet colormap from Matlab in gnuplot. Since Matlab R2014b jet is no longer the default colormap. Now parula is the new default colormap. It was introduced together with new default line colors.

The changes in the default colormap address some of the points that were criticized of jet by Moreland and corrected by his colormap.

Fig. 1 Photoluminescence yield plotted with the parula colormap from Matlab (code to produce this figure, parula.pal, data)

A colormap similar to the original is stored in the parula.pal file, which is also part of the gnuplot-palettes repository on github. An example application of the colormap is presented in Fig. 1.

In order to apply the colormap you can simply load the file.

load 'parula.pal'

The parula.pal file also includes definitions of line styles. The first line styles (1-9) corresponds to the colors of the parula palette, the line styles 11-17 correspond to the new Matlab line colors, see Fig. 2.

Fig. 2 Bessel functions from order zero up to six plotted with the new default Matlab line colors. (code to produce this figure, parula.pal, data)

set style line 11 lt 1 lc rgb '#0072bd' # blue
set style line 12 lt 1 lc rgb '#d95319' # orange
set style line 13 lt 1 lc rgb '#edb120' # yellow
set style line 14 lt 1 lc rgb '#7e2f8e' # purple
set style line 15 lt 1 lc rgb '#77ac30' # green
set style line 16 lt 1 lc rgb '#4dbeee' # light-blue
set style line 17 lt 1 lc rgb '#a2142f' # red

If you want to use only the palette and not the line colors, you should remove them from the parula.pal file.

Tags: colormap, linestyle, load, Matlab, palette

September 29th, 2014 | 6 Comments

Some time ago I introduced already a waterfall plot, which I named a pseudo-3D-plot. In the meantime, I have been asked several times for a colored version of such a plot. In this post we will revisit the waterfall plot and add some color to it.

Fig. 1 Waterfall plot of head related impulse responses. (code to produce this figure, color palette, data)

In Fig. 1 the same head related impulse responses we animated already are displayed in a slightly different way. They describe the transmission of sound from a source to a receiver placed in the ear canal dependent on the position of the source. Here, we show the responses for all incident angles of the sound at once. At 0° the source was placed at the same side of the head as the receiver.

The color is added by applying the Moreland color palette, which we discussed earlier. The palette is defined in an extra file and loaded, this enables easy reuse of defined palettes. In the plotting command the palette is enabled with the lc palette command, that tells gnuplot to use the palette as line color depending on the value of the third column, which is given by color(angle).

load 'moreland.pal'
set style fill solid 0.0 border
limit360(x) = x180?360-x:x
amplitude_scaling = 200
plot for [angle=360:0:-2] 'head_related_impulse_responses.txt' \
    u 1:(amplitude_scaling*column(limit360(angle)+1)+angle):(color(angle)) \
    w filledcu y1=-360 lc palette lw 0.5

To achieve the waterfall plot, we start with the largest angle of 360° and loop through all angles until we reach 0°. The column command gives us the corresponding column the data is stored in the data file, amplitude_scaling modifies the amplitude of the single responses, and +angle shifts the data of the single responses along the y-axis to achieve the waterfall.

Even though the changing color in the waterfall plot looks nice you should always think if it really adds some additional information to the plot. If not, a single color should be used. In the following the same plot is repeated, but only with black lines and different angle resolutions which also have a big influence on the final appearance of the plot.

Fig. 2 Waterfall plot of head related impulse responses with a resolution of 5°. (code to produce this figure, data)

Fig. 3 Waterfall plot of head related impulse responses with a resolution of 2°. (code to produce this figure, data)

Fig. 4 Waterfall plot of head related impulse responses with a resolution of 1°. (code to produce this figure, data)

Tags: data, fill, filledcurves, for, iteration, palette, style

June 23rd, 2014 | 8 Comments

Occasionally it is a good idea to create a zoom of some part of your main plot, especially if you have a small part of your plot where the data is hiding each other.

Fig. 1 Including a zoom into your figure to emphasize some data. (code to produce this figure, data)

In Fig. 1 the interaural time difference between a sound signal reaching the two ears of a listener is plotted with different colors for different frequencies. The data is very dense around 0°, so we include a zoom into this region in the same figure at a free place.

This can be done via multiplot and the plotting of the same data in a smaller figure.

set origin 0.12,0.17
set size 0.45,0.4
set xrange [-10:0]
set yrange [0:0.1]
plot for [n=2:13] 'itd.txt' u 1:(column(n)*1000) w lines ls n

The tricky part is that we have a grid in our main figure and if we do nothing the grid will also be visible in the zoomed in version as shown in Fig. 2.

Including a zoom with multiplot without grid correction

Fig. 2 Including a zoom into your figure, without correcting the grid. (code to produce this figure, data)

To avoid this we have to hide the grid in the background of the zoomed graph. This is done with the trick of placing an empty white rectangle at the place the zoom plot should appear in the figure.

set object 1 rect from -88,0.03 to -49,0.41
set object 1 rect fc rgb 'white' fillstyle solid 0.0 noborder

This will then finally lead to the desired result presented in Fig. 1.

Tags: data, grid, multiplot, object, rectangle, zoom

June 3rd, 2014 | No Comments

Suppose we have a file containing the following data from the plotting data tutorial:

# absolute_data.txt
# X   Y
1   2
2   3
3   2
4   1

Fig. 1 Plotting absolute data points. (code to produce this figure, data)

This can be plotted in a straightforward manner and will result in Fig. 1. Now suppose we have the same data points stored as relative coordinates in our data file, resulting in:

# relative_data.txt
# deltaX deltaY
1   2
1   1
1   -1
1   -1

If we want to plot that data in gnuplot we have to keep track of the current position manually by storing its (x,y) value as variables by

x=0.; y=0.
plot 'relative_data.txt' u (x=x+$1):(y=y+$2) w p ls 1

Here, we define the starting point to be (0,0) and add to it the values from the first and second column for every line of the data file. By doing so, this results again in Fig. 1. Note, that the addition is always performed first, before the resulting point is plotted which means we get no point at (0,0). Now assume that we also want to add steps going from point to point as shown in Fig. 2. Gnuplot has the steps plotting style to achieve this, but we have to be carefully regarding our (x,y) variables.

Fig. 2 Plotting relative data points. (code to produce this figure, data)

Every single line of a plotting command is executed after each other which means our (x,y) pair will not be set to (0,0), but to (4,1) at the beginning of the second line of the plotting command. To avoid this we introduce another (a,b) pair for the second line and get finally.

x=0.; y=0.
a=0.; b=0.
plot 'relative_data.txt' u (x=x+$1):(y=y+$2) w steps ls 2,\
     ''                  u (a=a+$1):(b=b+$2) w points ls 1

Tags: data, points, relative, steps, variable

April 16th, 2014 | 17 Comments

Gnuplot comes with the possibility of plotting histograms, but this requires that the data in the individual bins was already calculated. Here, we start with an one dimensional set of data that we want to count and plot as an histogram, similar to the hist() function we find in Octave.

Fig. 1 Two different distributions of measured angles. (code to produce this figure, hist.fct, data)

In Fig. 1 you see two different distributions of measured angles. They were both given as one dimensional data and plotted with a defined macro that is doing the histogram calculation. The macro is defined in an additional file hist.fct and loaded before the plotting command.

binwidth = 4
binstart = -100
load 'hist.fct'
plot 'histogram.txt' i 0 @hist ls 1,\
     ''              i 1 @hist ls 2

The content of hist.fct, including the definition of @hist looks like this

# set width of single bins in histogram
set boxwidth 0.9*binwidth
# set fill style of bins
set style fill solid 0.5
# define macro for plotting the histogram
hist = 'u (binwidth*(floor(($1-binstart)/binwidth)+0.5)+binstart):(1.0) smooth freq w boxes'

For a detailed discussion on why @hist calculates a histogram you should have a look at this discussion and the documentation about the smooth freq which basically counts points with the same x-value. The other settings in the file define the width of a single bin plotted as a box and its fill style.

Fig. 2 Two different distributions of measured angles. The bins of the histograms are shifted to be centered around 0°. (code to produce this figure, hist.fct, data)

It is important that the two values binwidth and binstart are defined before loading the hist.fct file. These define the width of the single bins and at what position the left border of a single bin should be positioned. For example, let us assume that we want to have the bins centered around 0° as shown in Fig. 2. This can be achieved by settings the binstart to half the binwidth:

binwidth = 4
binstart = -2
load 'hist.fct'
plot 'histogram.txt' i 0 @hist ls 1,\
     ''              i 1 @hist ls 2

Tags: boxes, histogram, index, load, macros

February 21st, 2014 | 5 Comments

For the measurement of distances T-shaped arrows are often used to highlight the length. In gnuplot there is an easy way to achieve this.

$Diffraction on a slit$

Fig. 1 Diffraction of light for a slit with the length d. (code to produce this figure)

Have a look at Fig. 1 which tries to explain the diffraction phenomenon of a slit with the length d. At a distance a the diffraction pattern is drawn. The different distances, the distance between the first minima of the diffraction pattern, and the wave length are indicated by T-shaped arrows. This kind of arrays can be achieved in gnuplot with the following code.

Theads = 'heads size 0.5,90 front ls 201'
set arrow from -24,-2 to -24, 2       @Theads
set arrow from -22, 2 to -21.44,1.92  @Theads
set arrow from 1.5,-pi to 1.5,pi      @Theads
set arrow from -22,2.5*pi to 0,2.5*pi @Theads

Here, 90 is the relevant entry after size as it describes the opening angle of the arrow head.
In addition, an open circle is drawn to indicate the angle θ. This is achieved by specifying the opening angle for the circle object.

set object circle at -22,0 size 6 arc [-8:0]

Tags: arrow, circle, head, italic, object, table

Gnuplotting

Gnuplot Links

Circular heat map

Matplotlib colormaps

Labels with white background in LaTeX terminals

Ease your plotting with config-snippets

Matlab colorbar parula with gnuplot

Waterfall plots with changing color

Zooming in with multiplot

Plotting relative data

Calculating histograms

Arrow with T-shaped head